Span & Co

Комбинация векторов

Комбинация векторов в Rⁿ - можно ли получить определённый вектор из других векторов,путём умножения каждого из них на любые реальные числа и суммирования. например:

b=a₁v₁+a₂v₂+...+a_nv_n

b-"определённый вектор" v-"другие вектора" a-"любые реальные числа."

Комбинация векторов , так же маршрут из 0 a ₁ раз вдоль вектора v ₁ a потом a ₂ раз в v ₂.

Что бы понять является ли вектор комбинацией других векторов нужно доказать , что b=a₁ v₁ +a₂v₂+...+a_nv_n имеет одно или множество решений. Для этого надо решить расширенную матрицу соответствующую этому уравнению.

Пример №2

Даны два вектора (1 ,0, 0) и (0,1,0). Какие комбинации векторов можно получить? Все комбинации данных векторов можно представить , как (n,m,0)

Span

Все комбинации имеющихся векторов в Rⁿ называются Span . То есть в примере №2 span(n,m,0)=sp(n,m,0).

В каждый Span входит нулевой вектор. Так как 0*v₁ + 0* v₂ =0 или 0*(1,2,3)+1*(3,4,5)=(3,4,5)

Что бы узнать находится ли вектор "b" в Span нужно решить уравнение b=a₁v₁+a₂v₂+...+a_nv_n . Если есть одно или несколько решений , то вектор находится в Span. То есть он является их линейной комбинацией.

Геометрическое представления span

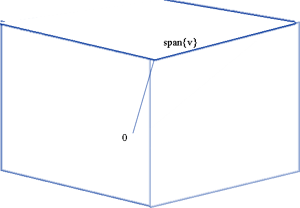
Span{v}- Набор из умножение любых реальных чисел на v или прямая в 3D исходящая из 0.

Span{v,u}- Плоскость между векторами v и u в 3D один из углов которой в 0.